基于GNFA-SVR污水出水总氮软测量研究

doi:10.19965/j.cnki.iwt.2021-1250

基于GNFA-SVR污水出水总氮软测量研究

郭利进^,, 李博仑^,

天津工业大学控制科学与工程学院，天津 300387

Research on soft measurement of effluent total nitrogen based on GNFA-SVR

GUO Lijin^,, LI Bolun^,

School of Control Science and Engineering，Tiangong University，Tianjin 300387，China

收稿日期: 2022-07-25

基金资助:

国家自然科学基金面上项目. 61973234

Received: 2022-07-25

作者简介 About authors

郭利进（1970—），博士，教授电话：13821101965，E-mail：Doctor_guo@tiangong.edu.cn , E-mail：Doctor_guo@tiangong.edu.cn

李博仑，硕士研究生电话：15612184192，E-mail：15612184192@163.com , E-mail：15612184192@163.com

摘要

污水处理流程具有滞后性、时变性、强耦合、非线性等特点，是一个多维输入、多维输出的复杂系统。根据实时进水水质判断未来出水水质的一些参数是否存在超标可能，以便提前对工艺参数进行调整，对污水处理系统的优化具有重要意义。针对污水处理出水总氮（TN）检测大滞后的问题，提出一种基于高斯函数非线性递减步长的萤火虫算法优化支持向量回归参数（GNFA-SVR）的软测量模型。通过改进萤火虫算法（FA）对支持向量回归机（SVR）的惩罚因子和核参数寻优，将污水进水水质的特征组分作为预测模型输入，建立GNFA-SVR出水TN预测模型。仿真结果表明，与LFA（线性递减步长的萤火虫算法）-SVR和FA-SVR预测模型相比，GNFA-SVR组合模型参数寻优收敛速度快、预测精度高，且预测误差在±0.5 mg/L以内，可实现出水TN的精准预测。

关键词： 萤火虫算法 ; 支持向量回归机 ; 参数优化 ; 出水总氮 ; 预测模型 ; 高斯函数

Abstract

The sewage treatment process has the characteristics of hysteresis，time-varying，strong coupling and nonlinearity. It is a complex system with multi-dimension input and multi-dimension output. According to the real-time influent quality，it is possible to judge whether some parameters of the future effluent quality exceed the standard，so as to adjust the process parameters in advance，which is of great significance to the optimization of the sewage treatment system. In order to solve the problem of long lag in the detection of total nitrogen（TN） in wastewater，a soft sensor model，based on Gaussian function nonlinear decreasing step firefly algorithm，was proposed to optimize support vector regression parameters（GNFA-SVR）. The improved firefly algorithm（FA） was used to optimize the penalty factor and kernel parameters of SVR. The characteristic components of influent quality were taken as the input of the prediction model to establish the GNFA-SVR total nitrogen of effluent prediction model. Simulation results showed that compared with LFA（linear decreasing step firefly algorithm）-SVR and FA-SVR prediction model，the GNFA-SVR model had fast convergence speed and high prediction accuracy，and the prediction error was within ±0.5 mg/L，which could achieve accurate prediction of total nitrogen of effluent.

Keywords： firefly algorithm ; support vector regression ; parameter optimization ; total nitrogen of effluent ; prediction model ; Gaussian function

PDF (1655KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

郭利进, 李博仑. 基于GNFA-SVR污水出水总氮软测量研究. 工业水处理[J], 2022, 42(10): 111-117 doi:10.19965/j.cnki.iwt.2021-1250

GUO Lijin. Research on soft measurement of effluent total nitrogen based on GNFA-SVR. Industrial Water Treatment[J], 2022, 42(10): 111-117 doi:10.19965/j.cnki.iwt.2021-1250

氮是微生物繁殖的必要元素，但也是引发水体富营养化的元素之一^〔1〕。出水总氮（TN）是污水排放的重要指标之一，当出水TN检测结果不达标时，污水厂会采取应急措施，通过调整某个工艺段的工艺参数来解决问题。因此，根据实时进水水质情况判断未来出水TN是否存在超标可能并提前对工艺参数进行调整，对污水处理系统的优化具有重要意义。

在污水水质预测创建模型方面，众多学者从污水处理过程机理和数据驱动方式去构建模型。O. S. DJANDJA等^〔2〕提出一种根据生化反应温度与原料中元素含量关系的前馈神经网络氮含量预测模型。乔俊飞等^〔3〕采用一种基于递归径向基（RBF）神经网络算法的氨氮软测量方法。尽管神经网络算法在预测领域有着不错的性能表现，但也存在一定局限性，如收敛速度慢、易陷入局部极值、过度拟合等^〔4〕。

与神经网络算法相比，支持向量回归机（SVR）具有训练时间短、泛化能力强、预测精度高的优点，并且克服了神经网络算法在小样本、非线性问题中的重复性差、过度拟合等不足，更适用于预测研究^〔5-8〕。然而，SVR模型构建的关键是解决核参数σ和惩罚因子c的最优取值问题，初期算法的参数选取多依赖于主观经验，缺乏严谨的数学依据。本研究通过引入基于高斯函数递减步长的萤火虫算法（GNFA）对SVR参数进行优化，可有效提高模型的预测准确度。

1 基本原理

1.1 支持向量回归机

支持向量回归机（SVR）是一种监督性机器学习算法，是在支持向量机（SVM）理论基础上延伸出的一种对回归分析问题的应用模型。SVR通过引入不敏感损失系数ε让所有的样本点与超平面距离和最小，得到一个最佳条状区域（2ε宽度），以达到期望风险最小的目的^〔9〕。

给定n个训练样本 $D = \{(x_{i}, y_{i}) | i = 1,2, \dots, n\}$ ，且 $x_{i} \in R^{n}, y_{i} \in R^{n}$ ， $x_{i}$ 为预测模型的相关输入向量， $y_{i}$ 为对应的输出向量，构造回归决策函数，见式（1）。其中，ω是权向量； $φ (x)$ 是原始样本数据的非线性映射函数，可将数据映射至特征空间；b为偏置值。

f (x) = ω^{T} φ (x) + b

（1）

引入不敏感损失系数ε与惩罚因子c， $y_{i}$ 为实际值， $f (x_{i})$ 为模型的输出预测值，当 $y_{i}$ 与 $f (x_{i})$ 差的绝对值大于ε时计算损失；反之则认为预测正确，不计算损失^〔10〕。不敏感损失系数ε对模型影响较小，选取0.15即可。根据最小结构风险原则，建立约束条件〔式（2）〕与目标函数〔式（3）〕。

L [f (x_{i}), y_{i}, ε] = \{\begin{array}{l} 0 | y_{i} - f (x_{i}) | \leq ε \\ | y_{i} - f (x_{i}) | - ε | y_{i} - f (x_{i}) | > ε \end{array}

（2）

\underset{ω, b}{m i n} J (ω, b) = \frac{1}{2} | | ω | |^{2} + c \sum_{i = 1}^{n} | y_{i} - f (x_{i}) |

（3）

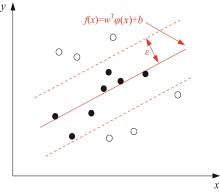
图1为SVR的示意图，黑色实心的数据点表示模型预测结果是有效的。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 支持向量回归示意

Fig. 1 Support vector regression diagram

惩罚因子c的取值影响模型的结构风险，取值过大，结构风险越大，模型容易出现过拟合；取值过小，模型会过于简单化，易出现欠拟合问题^〔11〕。

引入松弛变量 $ξ_{i}$ 与 $ξ_{i}^{*}$ ，建立新的目标函数〔式（4）〕。

\{\begin{array}{l} \underset{ω, b}{m i n} \frac{1}{2} {‖ω‖}^{2} + c \sum_{i = 1}^{m} (ξ_{i} + ξ_{i}^{*}) \\ s . t . \{\begin{array}{l} y_{i} - ω φ (x) - b \leq ε + ξ_{i} \\ - y_{i} + ω φ (x) + b \leq ε + ξ_{i}^{*} \\ ξ_{i} \geq 0, ξ_{i}^{*} \geq 0 \end{array} \end{array}

（4）

引入拉格朗日乘子 $α$ 、 $α_{}^{*}$ ，将式（4）变换为对偶形式〔式（5）〕。式中， $K (x_{i}, x_{j}) = φ (x_{i}) φ (x_{j})$ 为核函数。

\{\begin{array}{l} \underset{α, α^{*}}{m a x} [\begin{array}{l} \sum_{i = 1}^{n} y_{i} (α_{i} - α_{i}^{*}) - ε \sum_{i = 1}^{n} (α_{i} - α_{i}^{*}) \\ - \frac{1}{2} \sum_{i = 1}^{n} \sum_{j = 1}^{n} (α_{i} - α_{i}^{*}) (α_{j} - α_{j}^{*}) K (x_{i}, x_{j}) \end{array}] \\ s . t . \sum_{i = 1}^{n} (α_{i} - α_{i}^{*}) = 0 \end{array}

（5）

根据式（5）的函数关系式可求出 $α$ 与 $α^{*}$ ，最终可得到回归函数，表达式见式（6）。

f (x) = \sum_{i = 1}^{m} (α_{i} - α_{i}^{*}) K (x_{i}, x_{j}) + b

（6）

映射时发现，当变量增多时，映射到高维空间的维度呈指数增长，导致计算难度骤增；而引入核函数可使低维计算结果等效于高维。核函数根据需要选取，研究中选用径向核函数，表达式见式（7）。σ为径向核函数的核参数，其取值大小也会影响模型效果，取值过小会导致模型的泛化能力减弱，取值过大会令模型出现过拟合现象。

K (x_{i}, x_{j}) = e x p [- (x_{i} - x_{j})^{2} / 2 σ^{2}]

（7）

综上，SVR模型构建的关键是解决核参数σ和惩罚因子c的最优取值问题。

1.2 改进萤火虫算法

萤火虫算法（FA）是一种启发式算法，是根据自然界中萤火虫的发光行为提出的^〔12〕。在FA中，空间里的每一个解就好比萤火虫种群里的每一只萤火虫，空间里的初始解可以理解为萤火虫种群的初始位置，萤火虫通过个体之间的吸引进行移动，完成位置的更新，即完成解的更新^〔13〕。

搜索过程涉及到萤火虫的发光亮度和相互吸引度^〔14〕，这2个参数都与萤火虫之间的距离成反比，这与自然现象中光在空间传播时被传播介质吸收而逐渐衰减的特性一致。

FA算法中萤火虫发光强度的计算公式见式（8）。

I_{r} = I_{0} e^{- γ r_{i j}^{2}}

（8）

式中， $I_{r}$ 表示发光强度； $r_{i j}$ 表示萤火虫 $i$ 与萤火虫 $j$ 之间的距离， $r_{i j}^{} = | | X_{i} - X_{j} | |$ ；吸收系数γ的改变可以理解为传播介质的改变，可设置为常数；当萤火虫个体与光源的距离逐渐趋近于0时，萤火虫的发光亮度最为明亮，即为 $I_{0}$ ^〔15〕。

萤火虫的吸引度 $β$ 见式（9），与萤火虫发光强度同理，当萤火虫个体与光源的距离逐渐趋近于0时，吸引度最大，即为 $β_{0}$ ^〔16〕。

β = β_{0} e^{- γ r_{i j}^{2}}

（9）

萤火虫 $i$ 被吸引向萤火虫 $j$ 移动的位置更新由式（10）决定。

X_{i}^{'} = X_{i} + β (X_{j} - X_{i}) + α (r a n d - 0.5)

（10）

式中， $X_{i}^{'}$ 为下一次迭代的位置； $α (r a n d - 0.5)$ 为扰动项； $α$ 为步长因子，是介于0~1之间的常数； $r a n d$ 是［0，1］上服从均匀分布的随机因子。扰动项的加入是为了扩大寻优区域^〔17〕。

在文献〔18〕中，优化粒子群算法引入了线性递减权重。受该思路启发，不妨将萤火虫的步长进行线性递减优化，定义该种改进算法为线性递减步长萤火虫算法（LFA），具体步长变化表达式见式（11）。

α = α_{m a x} - \frac{α_{m a x} - α_{m i n}}{T_{m a x}} \times t

（11）

式中， $α$ 是步长； $α_{m a x}$ 是最初步长； $α_{m i n}$ 是最终步长； $t$ 为当前迭代次数； $T_{m a x}$ 为设置的最大迭代次数。

因为FA算法在实际问题的寻优过程中是复杂非线性的，所以步长也呈动态非线性变化预计会出现较好的寻优结果。结合高斯函数分布的特性，猜想当步长的随机变化呈正态分布时，能够提高算法的寻优精度。因此，根据高斯函数分布特性，把相应的步长参数带入步长变化表达式，实现对步长 $α$ 的非线性映射，得到最终的高斯递减函数调整步长策略，见式（12）。

α (t) = (α_{m a x} - α_{m i n}) e x p [- \frac{t^{2}}{k T^{2}}] + α_{m i n}

（12）

式中，常数k可以影响曲线的凹凸程度，即曲线的变化率可通过k进行调整。

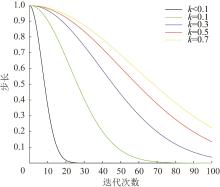
以步长取值范围为0~1、最大迭代次数为100时为例，图2给出了不同k值对应步长的变化曲线。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 k取不同值时步长的变化

Fig. 2 Change of step with different k

由图2可看出，当k≤0.1时，步长过早收敛于0，导致寻优效果过于局限；当k≥0.3时，步长在整个迭代过程中的变化趋势较为平缓，不利于算法收敛。所以本研究中k取0.2，高斯函数递减步长的萤火虫算法（GNFA）位置更新表达式见式（13）。

\{\begin{array}{l} X_{i}' = X_{i} + β (X_{j} - X_{i}) + α (r a n d - 0.5) \\ α = (α_{m a x} - α_{m i n}) e x p [- \frac{t^{2}}{k T^{2}}] + α_{m i n}, k = 0.2 \end{array}

（13）

2 GNFA算法性能测试

为验证改进算法的性能，分别将FA、LFA与提出的GNFA进行比较。选择Sphere函数和Ackley函数作为测试算法性能的函数，Sphere函数多用来检验算法的收敛速度和精度，Ackley函数可以测试算法的局部寻优能力。这2个函数是最常见的测试函数，被广泛应用在算法测试性能实验中^〔19〕。

在仿真环境中，萤火虫步长改进优化算法的具体参数设置为：萤火虫数目M=20，光强吸收系数γ=1.0，初始吸引度 $β_{0}$ =0.8，步长因子 $α_{m a x}$ 、 $α_{m i n}$ 分别设置为0.8、0.1，最大迭代次数T=500， $α$ 的变化停止阈值Th设置为10^-3。而FA算法步长设置为0.4，其他参数和改进算法设置一致。测试函数的搜索范围、期望目标值、搜索空间维数及函数类型等见表1。

表1 测试函数特征

Table 1 Test function characteristics

函数	维数	搜索范围	期望目标值	函数类型
Sphere	10	［-100，100］	0	单峰函数
Ackley	15	［-32，32］	0	多峰函数

新窗口打开| 下载CSV

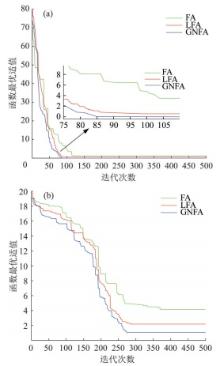
测试函数的优化结果见表2，平均最优值随迭代次数增加的变化曲线见图3。

表2 测试函数的优化结果

Table 2 The optimization results of the test functions

函数	结果	FA	LFA	GNFA
Sphere	最优值	1.241 9	0.057 5	1.08×10^-16
	平均适值	2.014 8	0.078 9	1.52×10^-12
	标准差	1.113 7	0.097 9	4.08×10^-12
	执行时间/s	10.16	8.07	7.84
Ackley	最优值	4.125 6	2.184 6	1.059 6
	平均适值	6.271 8	3.233 1	2.916 7
	标准差	2.726 5	2.141 8	1.466 3
	执行时间/s	13.267 4	11.093 2	10.77

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 Sphere函数（a）和Ackley函数（b）收敛曲线

Fig. 3 Convergence curves of Sphere function（a） and Ackley function （b）

从表2的优化结果可看出，相比LFA与标准FA算法，GNFA算法综合表现更佳，说明当采用高斯非线性递减方式改进步长策略时，萤火虫个体寻优性能强，且算法执行时间也得到优化。

从图3可看出，3种算法对单峰值Sphere函数的优化结果在寻优精度上相差不大，但GNFA收敛速度快于其他2种算法。3种算法对多峰值Ackley函数的优化结果说明，在迭代后期，标准FA算法定值步长容易导致算法陷入局部最优；而LFA算法的性能表现介于其他2种算法。虽然线性递减改进步长策略并非最好的优化方式，但也说明了步长 $α$ 是影响算法性能的一个关键参数。总之，与传统FA算法相比，GNFA算法在局部寻优能力、全局搜索精度及收敛速度方面都得到改善。

3 基于GNFA-SVR的TN软测量建模

3.1 模型数据选取与处理

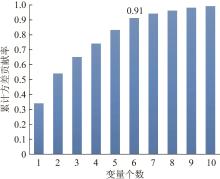
如果进水水质组分全部被选作特征向量，其中部分特征变量存在弱相关性的问题往往会被忽视，导致维度过高，模型的计算时间和计算难度增加，不利于模型预测结果分析。主成分分析（PCA）是一种对高维度特征数据降维的统计分析法，有利于确定特征变量维数。图4为使用PCA对数据特征变量进行降维分析的相关度，当选取6个特征变量时，总体的累计方差贡献率已经达到了90%。故本研究选取6个特征变量：进水COD、TN、NH₄⁺-N、温度（T）、浊度（SS）、DO，并以出水总氮（TN）作为模型输出。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 累计方差贡献率

Fig. 4 Cumulative variance contribution rate

从某污水厂2021年6月至9月水质信息库共获取657组样本数据，部分采集数据见表3。其中200组数据作为测试数据用于检验模型性能，457组数据作为训练集用于预测模型训练。

表3 部分采集数据

Table 3 Part of collected data

组号	进水COD/（mg·L^-1）	进水TN/（mg·L^-1）	进水NH₄⁺-N/（mg·L^-1）	进水SS/（mg·L^-1）	进水温度/℃	进水DO/（mg·L^-1）	出水TN/（mg·L^-1）
1	49.9	51.5	23.1	165.4	25.3	0.81	10.6
2	43.3	42.9	19.5	153.4	28.4	0.64	9.2
3	59.4	48.9	17.7	185.4	26.2	0.73	10.9
4	61.2	58.0	19.8	148.3	32.5	0.98	12.0
5	47.8	57.7	22.2	163.3	24.1	1.22	11.3
6	63.1	47.1	20.4	169.3	22.3	1.41	12.1
7	82.5	49.0	22.1	173.2	25.0	1.02	13.2
8	72.7	39.1	17.2	205.5	30.2	0.79	11.1
9	51.5	46.3	19.7	164.2	31.3	0.95	12.3
10	49.1	37.9	14.7	197.3	30.8	1.31	9.6

新窗口打开| 下载CSV

样本数据通常不直接使用，因为不同类型数据的量纲不同；且样本数值波动较大时，不利于模型的学习训练。为消除特征向量间的量纲影响、保证模型运行速度以及提高预测精度，需对训练样本数值进行归一化处理。归一化公式见式（14）。

x^{'} = \frac{x - m i n (x)}{m a x (x) - m i n (x)}

（14）

式中， $x$ 是任意一组样本的某一维数据，最大值用 $m a x (x)$ 表示，最小值用 $m i n (x)$ 表示， $x^{'}$ 为归一化后的数据。

3.2 算法流程

步骤1：将经过预处理后的n组水质样本数据 $(x_{1}, y_{1}), (x_{2}, y_{2}), \dots, (x_{n}, y_{n})$ 归一化，并将其分为训练集和测试集2部分。

步骤2：对GNFA算法参数进行初始化设置，包括萤火虫数量M、初始吸引度 $β_{0}$ 、光强吸收系数γ、步长因子上下限 $α_{m a x}$ 和 $α_{m i n}$ 、最大迭代次数T。

步骤3： $[c, σ]$ 作为SVR的初始参数，也代表萤火虫的1个位置；将训练集样本作为SVR模型的输入，并输出预测集 ${{\hat{y}}_{i}, \dots, {\hat{y}}_{n}}$ 。

步骤4：将预测值与实际值的均方根误差作为GNFA-SVR算法的适应度。

步骤5：判断终止条件，即当前迭代次数是否大于设置的最大迭代次数；满足终止条件执行步骤7，不满足则执行下一步骤。

步骤6：根据萤火虫的相对亮度决定下一个位置的移动方向并调整步长 $α$ ；若目标位置劣于之前的位置，萤火虫位置保持不变，否则萤火虫进行位置更新，产生新的 $[c, σ]$ ，返回步骤3。

步骤7：将输出的最优解［ $c^{*}, σ^{*}$ ］代入SVR预测模型，利用测试集检验算法的准确性和可靠性，评估预测模型性能。

3.3 污水厂出水TN预测

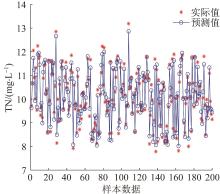
设置模型参数：萤火虫数目M=40，光强吸收系数γ=1.0，初始吸引度β₀=0.8，步长因子α_max=0.8、α_min=0.1，最大迭代次数T=600，α变化停止阈值Th=10^-3，惩罚因子c取值范围为［0.01，1 000］，σ取值范围为［0.001，10］。在MATLAB R2018b环境下借助支持向量回归机工具箱运行GNFA-SVR模型。基于GNFA-SVR模型对测试集的出水TN预测结果见图5，GNFA-SVR可以较好地预测出水TN的实际值，预测误差较小。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 出水TN预测结果

Fig. 5 Prediction results of total nitrogen in effluent

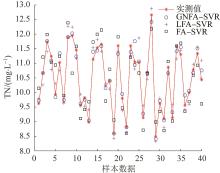
为进一步验证3种算法在实际问题上对SVR算法的优化效果，现用GNFA-SVR、LFA-SVR和FA-SVR这3种预测算法对出水TN进行预测。部分测试样本的预测结果见图6，其中GNFA-SVR与LFA-SVR的模型参数设置同上；FA-SVR所需参数步长α=0.4，其他参数和GNFA-SVR算法设置一致。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 出水TN预测结果对比

Fig. 6 Comparison of predicted results of TN in effluent

从3种模型预测对比图（图6）可看出，3种模型的预测值与实测值的变化趋势基本一致，其中GNFA-SVR模型预测值与实测值拟合效果最佳，预测误差最小。

对3种模型的性能进行具体评估，采用平均绝对误差（MAE）、最大误差（Maxer）和均方根误差（RMSE）对预测结果进行评定，表达式见式（15）~（17）。

M A E = \frac{1}{N} \sum_{i = 1}^{N} | ({\hat{y}}_{i} - y_{i}) |

（15）

M a x e r = m a x |y_{i} - {\hat{y}}_{i}|

（16）

R M S E = \sqrt[]{\frac{1}{N} \sum_{i = 1}^{N} {(y_{i} - {\hat{y}}_{i})}^{2}}

（17）

式中，N为样本总个数； ${\hat{y}}_{i}$ 为预测值； $y_{i}$ 为实际值。

3种预测模型的评价指标见表4。

表4 不同预测模型的评价指标

Table 4 Evaluation indicators of different prediction models

出水水质	模型	MAE	Maxer	RMSE
TN	FA-SVR	0.621 1	0.993 4	0.894 6
	LFA-SVR	0.387 2	0.532 5	0.468 1
	GNFA-SVR	0.352 1	0.381 6	0.329 3

新窗口打开| 下载CSV

由表4可知，GNFA-SVR算法预测结果的各项指标均优于其他2种算法，其中MAE为0.352 1，预测误差控制在±0.5 mg/L以内可满足污水厂实际生产需求；RMSE较LFA-SVR算法与FA-SVR算法分别降低了29.7%、63.2%。说明GNFA-SVR组合模型在改进策略的优化下预测性能有所提升，可实现对出水TN的精准预测。

4 结论

针对污水处理厂出水水质检测存在大滞后性的问题，本研究提出一种基于GNFA-SVR算法的预测模型。在SVR算法基础上，引入萤火虫算法对其进行参数寻优。针对标准FA算法的步长不随迭代次数变化、易出现陷入局部最优的现象，提出基于高斯函数非线性递减步长策略，有效提高了算法的性能。通过对污水处理厂的实际数据进行仿真验证，GNFA-SVR算法在平均绝对误差、最大误差和均方根误差3个评价指标方面均明显优于LFA-SVR与FA-SVR算法，预测精度最高，误差控制在±0.5 mg/L以内，可实现对出水TN的精准预测，在实际水质预测方面具有良好的应用前景。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李海华，鄂正阳，史振涛，等.

基于总氮达标的河南省某污水处理厂提标改造工艺研究

［J］. 水处理技术，2021，47（4）：137-140. doi:10.16796/j.cnki.1000-3770.2021.04.028